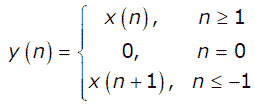-
163.
X(t) is a random process with a constant mean value of 2 and the autocorrelation function
Rx(τ) = 4 [e-0.2|τ| + 1].
[1] Let X be the Gaussian random variable obtained by sampling the process at t = ti and let 
The probability that [x ≤ 1] is [2 marks]
(a) 1 – Q(0.5)
(b) Q(0.5)
(c) Q(1/2√2)
(d) 1- Q(1/2√2)
[2] Let Y and Z be the random variables obtained by sampling X(t) at t =2 and t = 4 respectively. Let W = Y – Z. The variance of W is [2 marks]
(a) 13.36
(b) 9.36
(c) 2.64
(d) 8.00asked in Electronics and Communication Engineering, 2003
View Comments [0 Reply]
-
164.
The system under consideration is an RC low-pass filter (RC-LPF) with R = 1.0 kΩ and C = 1.0µF.
[1] Let H(f) denote the frequency response of the RC-LPF. Let f1 be the highest frequency such that 0 ≤ |f| ≤ f1, |H(f1)|/H(0) ≥ 0.95. Then f1 (in Hz) is
[2 marks]
(a) 327.8
(b) 163.9
(c) 52.2
(d) 104.4[2] Let tg(f) be the group delay function of the given RC-LPF and f2 = 100 Hz. Then tg(f2) in ms, is [2 marks]
(a) 0.717
(b) 7.17
(c) 71.7
(d) 4.505asked in Electronics and Communication Engineering, 2003
View Comments [0 Reply]
-
165.
-
166.
-
167.
-
168.
In the circuit shown in Figure, A is a parallel in, parallel-out 4-bit register, which loads at the rising edge of the clock C. The input lines are connected to a 4-bit bus, W. Its output acts as the input to a 16×4 ROM whose output is floating when the enable input E is 0. A partial table of the contents of the ROM is as follows.
Address 0 2 4 6 8 10 12 14 Data 0011 1111 0100 1010 1011 1000 0010 1000 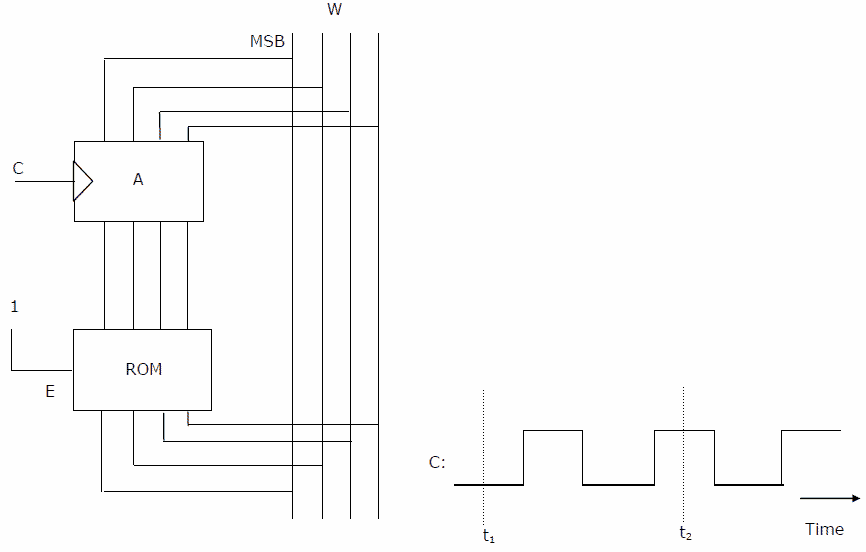
The clock to the register is shown, and the data on the W bus at time t1 is 0110. The data on the bus at time t2 is [2 marks]
(a) 1111
(b) 1011
(c) 1000
(d) 0010
asked in Electronics and Communication Engineering, 2003
View Comments [0 Reply]